Addition Algorithm Of Sign Magnitude Numbers

The resultant sum contains 5 bits. The signed binary number technique has both the sign bit and the magnitude of the number.

Bcd Addition Youtube

Where the signed numbers are added or subtracted we find that there are eight different conditions to consider depending on the sign of the numbers and the operation performed.

Addition algorithm of sign magnitude numbers. Determine the values of A and S and the initial value of P. 2s Complement Signed Numbers 0000 0000 0000 0000 0000 0000 0000 0000two 0ten 0000 0000 0000 0000 0000 0000 0000 0001two 1ten. Addition and Subtraction With Signed Magnitude Data.

Where the signed numbers are added or subtracted we find that there are eight different conditions to consider depending on the sign of the numbers and the operation performed. Fill the most significant leftmost bits with the value of m. If E 1 then A B.

If the sum is an overflow then a carry is stored in E where E 1 and transferred to the flip-flop AVF add-overflow. All of these numbers should have a length equal to x y 1. Eight Conditions for Signed- Magnitude AdditionSubtraction Operation ADD Magnit udes SUBTRACT Magnitudes A B A B A B A B A B A -B A B - B A A B -A B - A B B A A B -A -B - A B A - B A B - B A A B A - -B A B -A - B - A B.

Multiplication of two fixed point binary number in signed magnitude representation is done with process of successive shift and add operation. In the multiplication process we are considering successive bits of the multiplier least significant bit first. Operation Add Magnitudes Subtract Magnitudes.

If a four-bit signed-magnitude binary number represents x where x 0 then the bits of that representation have unsigned value 8 - lvert xrvert The sign bit has place value 8 and the rightmost three bits have value lvert xrvert The first step is to take the ones complement of the three magnitude bits which is equivalent to subtracting them from the three-bit number 111 that is from. We designate the magnitude of the two numbers by A and B. Numbers can be integers or floating point numbers.

So there is no carry out from sign bit. First we need to align the exponent and then we can add significand. The addition of these two numbers is 7 10 4 10 00111 2 00100 2 7 10 4 10 01011 2.

Now adding significand 005 11 115. The magnitude uses 7-bit unsigned binary which can represent 0 10 as 000 0000 up to 127 10 as 111 1111. Choose the sign of result to be same as A if AB or the complement of sign of A if A.

Negative numbers are represented using sign and magnitude or twos complement. The sign bit 0 indicates that the resultant sum is positive. No overflow can occur with subtraction so the AVF is cleared.

ADDITION ALGORITHM When the sign of A and B are same add the magnitudes and attach the sign of A to the result. The eighth bit makes these positive or negative resulting in -127 10. Now let us take example of floating point number addition.

Hence add the magnitudes of the same signed numbers. The leftmost bit is used for the sign which leaves seven bits for the magnitude. The sign-magnitude binary format is the simplest conceptual format.

If the multiplier bit is 1 the multiplicand is copied down else 0s are copied down. Otherwise the signs are opposite and subtraction is initiated and stored in A. In CPUs binary numbers need to be added together.

Like sign magnitude twos complement representation uses the most significant bit as a sign bit making it easy to test whether it is ve or ve. Here notice that we shifted 50 and made it 005 to add these numbers. -7 1 1 1 1 Sign Magnitude And its 2s complement is 1001 5 0 1 0 1 And its 2s complement is 0101 Addition- -7 1 0 0 1 -4 1 1 0 0.

After aligning exponent we get 50 005 10 3. 0111 1111 1111 1111 1111 1111 1111 1111two 231-1 1000 0000 0000 0000 0000 0000 0000 0000two -231 1000 0000 0000 0000 0000 0000 0000 0001two -231 1 1000 0000 0000 0000 0000 0000 0000 0010two -231 2. Addition and subtraction with signed magnitude data mano.

Otherwise compare the magnitudes and subtract the smaller number from the larger. And let x and y represent the number of bits in m and r. Division of signed magnitude fixed point numbers.

Multiplication and Division with Signed-Magnitude Data Module II. In this method of representing signed numbers the most significant digit MSD takes on extra meaning. So the magnitude of sum is 11 in decimal number system.

Therefore addition of two positive numbers will give another positive number. For representing the negative decimal number the corresponding symbol in front of the binary number will be added. Signed Numbers The signed numbers have a sign bit so that it can differentiate positive and negative integer numbers.

If the MSD is a 0 we can evaluate the number just as we would any normal unsigned integer. Fill the remaining y 1 bits with zeros. Division of signed magnitude fixed point numbers.

Let m and r be the multiplicand and multiplier respectively. So finally we get 11 10 3 50 115 10 3. Addition and Subtraction with Signed Magnitude Data We designate the magnitude of the two numbers by A and B.

Binary Addition And Subtraction With Negative Numbers 2 S Complements Signed Magnitude Youtube

2nd Grade Place Value Math Centers Third Grade Math Activities Kindergarten Math Activities Math Centers

2nd Grade Place Value Math Centers Math Centers Elementary School Math Activities Math

Computer Arithmetic Algorithm Algorithm Arithmetic Subtraction

2 Digit Addition Using The Expanded Form Strategy Second Grade Math Teaching Math Math Instruction

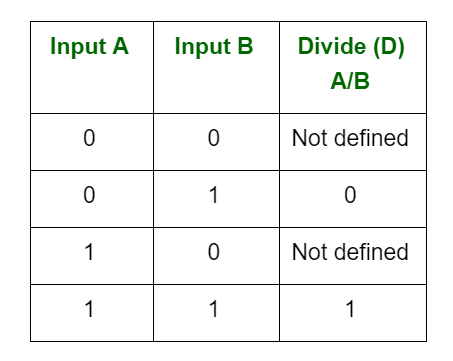Arithmetic Operations Of Binary Numbers Geeksforgeeks

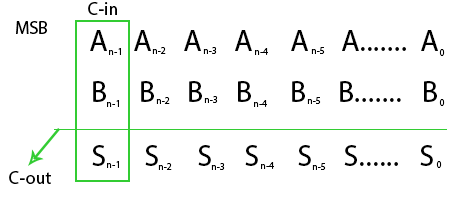Overflow In Arithmetic Addition In Binary Number System Geeksforgeeks

Mr J On Twitter Math Addition Math Place Value Mr

Difference Between Signed Magnitude And 2 S Complement Geeksforgeeks

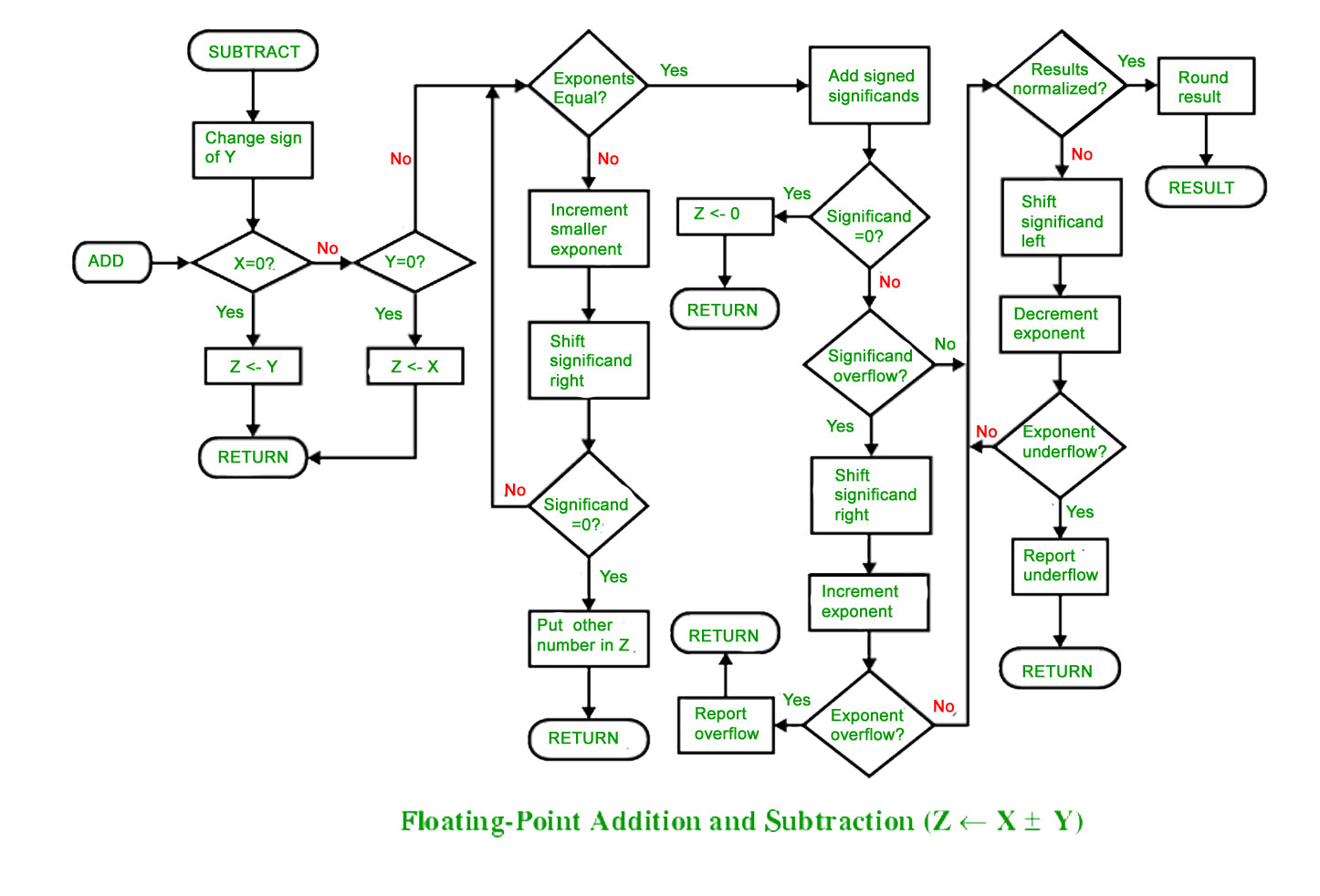Computer Arithmetic Set 2 Geeksforgeeks

2s Complement Arithmetic Electrical4u

Overflow In Arithmetic Addition In Binary Number System Geeksforgeeks

Tales From A Stage 3 Class Addition And Subtraction Mental Strategies Addition And Subtraction Addition Strategies Subtraction

Place Value Math Centers Elementary School Math Activities Elementary Math Math Centers

Adding Three Digit Numbers Anchor Chart Jessup Number Anchor Charts Anchor Charts Math Anchor Charts

Higher Order Thinking Questions For Kindergarten Math Google Search Higher Order Thinking Questions Higher Order Thinking Math

Magnitude And Direction Of A Vector Positive Numbers Absolute Value Directions

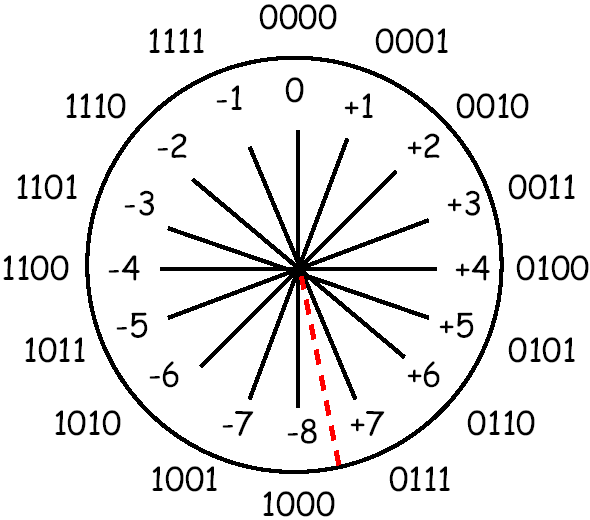Arithmetic Operations On Binary Numbers

Addition Strategies Anchor Chart Math Strategies Math Anchor Charts Math Addition